400-123-4567

• 导言
• 伪随机数产生方法
• 遗传算法(GA)
• 禁忌搜索(TS)
• 模拟退火(SA)
• 其他智能优化算法(神经网络，机器学习，深度学习等)
• Matlab与部分智能优化算法

参考书：

• 《智能优化方法》汪定伟 王俊伟 王洪峰 张瑞友 郭哲 编著,高等教育出版社
• 《智能优化算法原理与应用》李士勇 等编著, 哈尔滨工业 大学出版社
• Multi-Objective Optimization using Evolutionary Algorithms Kalyanmoy Deb, John Wiley & Sons, LTD

1 极值理论;
2 运筹学的兴起(Operation Research);
3 数学规划:线性规划(LP);非线性规划(NLP);动态 规划(DP);马尔可夫规划(MDP);排队论;决策论; 存储论。

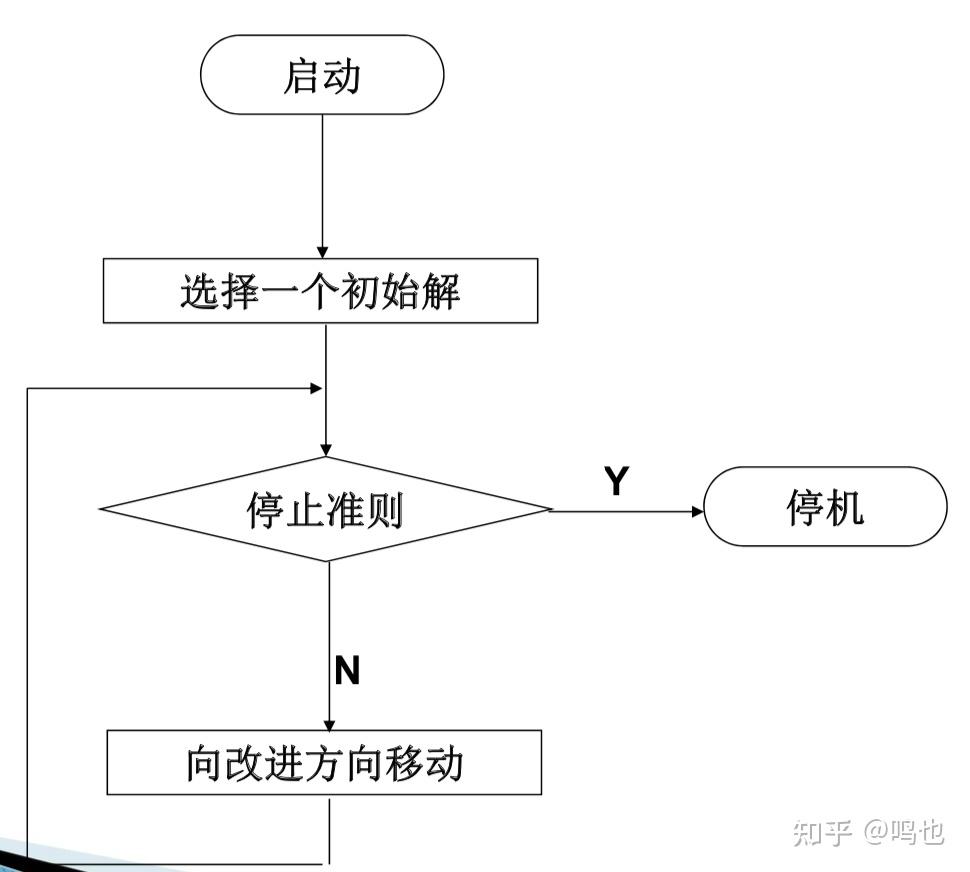
1. 对问题中目标函数、约束函数有很高的要求——有显式表达，线性、连续、可微，且高阶可微;

2. 只从一个初始点出发，难以进行并行、网络计算、分布式计算，难以提高计算效率;

3. 最优性达到的条件太苛刻——问题的函数为凸，可 行域为凸;

4. 在非双凸条件下，没有跳出局部最优解的能力。

现代优化算法又称智能优化算法或现代启发式算法， 是一种具有全局优化性能、通用性强、且适合于并 行处理的算法。

这种算法一般具有严密的理论依据,而不是单纯凭借专家经验，理论上可以在一定的时间内找到最优解或近似最优解。它们的共同特点：都是从任一解出发，按照 某种机制，以一定的概率在整个求解空间中探索 最优解。

由于它们可以把搜索空间扩展到整个问题空间，因而具有全局优化性能。

特点：

1)不依赖于初始条件;
2)不与求解空间有紧密关系,对解域无可微或连续的 要求;
3)容易实现，求解稳健;
4)但收敛速度慢,能获得全局最优;适合于求解空间未知的情况;
5)SA(Simulated Annealing),GA可应用于大规模、 多峰多态函数、含离散变量等全局优化问题;求解 速度和质量远超过常规方法。